A fair die is tossed repeatedly until a six is obtained. Let X denote the number of tosses required and let a = P(X = 3), b = P(X ≥ 3) and c = P(X ≥ 6 ∣ X > 3). Then b + c/a is equal to___
[27-Jan-2024 Shift 1]
An urn contains 6 white and 9 black balls. Two successive draws of 4 balls are made without replacement. The probability, that the first draw gives all white balls and the second draw gives all black balls, is :
[27-Jan-2024 Shift 2]
A fair die is thrown until 2 appears. Then the probability, that 2 appears in even number of throws, is
[29-Jan-2024 Shift 1]
An integer is chosen at random from the integers 1, 2, 3,...,50. The probability that the chosen integer is a multiple of atleast one of 4, 6 and 7 is
[29-Jan-2024 Shift 2]
Two integers x and y are chosen with replacement from the set {0, 1, 2, 3,....,10}. Then the probability that |x − y| > 5 is :
[30-Jan-2024 Shift 1]
Bag A contains 3 white, 7 red balls and bag B contains 3 white, 2 red balls. One bag is selected at random and a ball is drawn from it. The probability of drawing the ball from the bag A, if the ball drawn in white, is :
[30-Jan-2024 Shift 2]
Two marbles are drawn in succession from a box containing 10 red, 30 white, 20 blue and 15 orange marbles, with replacement being made after each drawing. Then the probability, that first drawn marble is red and second drawn marble is white, is
[31-Jan-2024 Shift 1]
Three rotten apples are accidently mixed with fifteen good apples. Assuming the random variable x to be the number of rotten apples in a draw of two apples, the variance of x is
[31-Jan-2024 Shift 1]
A coin is biased so that a head is twice as likely to occur as a tail. If the coin is tossed 3 times, then the probability of getting two tails and one head is-
[31-Jan-2024 Shift 2]
A bag contains 8 balls, whose colours are either white or black. 4 balls are drawn at random without replacement and it was found that 2 balls are white and other 2 balls are black. The probability that the bag contains equal number of white and black balls is:
[1-Feb-2024 Shift 1]
Let Ajay will not appear in JEE exam with probability p = 2/7, while both Ajay and Vijay will appear in the exam with probability q = 1/5. Then the probability, that Ajay will appear in the exam and Vijay will not appear is :
[1-Feb-2024 Shift 2]
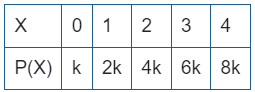
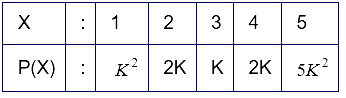

 ×
×