Calculation:

Statement I: (x + y)⁴ = 256

(x + y)⁴ = 16⁴

(x + y) = ± 4

So, no unique values of x, and y are possible from this statement alone.

Statement II: (x + y)³ < 16

No unique values of x, and y are possible from this statement alone.

Let's combine both statements

Let x = 4

(4)³ < 16

64 < 16 which is wrong

If x = -4

-64 < 16 which is correct.

So, (x + y) = - 4

∴ Optipon 3 is correct.

Given:

AB = 6 cm, BC = 10 cm, CA = 8 cm

Calculation:

Let the radii of the circles with A, B and C as centres be r₁, r₂ and r₃ respectively.

According to the given information,

AB = 6 cm = r₁ + r₃ ----(1)

BC = 10 cm = r₂ + r₃ ----(2)

CA = 8 cm = r₁ + r₂ ----(3)

Adding equations (1), (2) and (3),

⇒ 2(r₁ + r₂ + r₃) = 24

⇒ r1 + r2 + r₃ = 12 cm

∴ The sum of of the radii of the circle is 12 cm

Given:

AB = 6 cm ase

BC = 10 cm

CA = 8 cm

Formula used:

Area of triangle = 1/2 × base × height

Calculation:

Area of triangle ABC with base AB = Area of triangle ABC with base BC

(1/2) × 6 × 8 = (1/2) × 10 × AD

⇒ AD( altitude drawn from A to BC) = 4.8 cm

∴ The required answer is 4.8 cm.

Given:

AB = 6 cm, BC = 10 cm, CA = 8 cm

Concept:

Pythagoras theorem: In a right-angled triangle,

Hypotenuuse² = Base² + Perpedicular²

Calculation:

We have, AB = 6 cm, BC = 10 cm, CA = 8 cm

Using Pythagoras theorem,

AB² + AC² = 6² + 8² = 36 + 64

⇒ AB² + AC² = 100 = BC²

Therefore, Δ ABC is right-angled triangle with ∠A = 90°

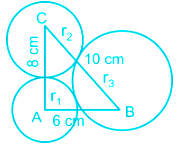
Let the radii of the circles with A, B and C as centres be r1, r2 and r3 respectively.

According to the given information,

AB = 6 cm = r₁ + r₃ ----(1)

BC = 10 cm = r₂ + r₃ ----(2)

CA = 8 cm = r₁ + r₂ ----(3)

Adding equations (1), (2) and (3),

⇒ 2(r₁ + r₂ + r₃) = 24

⇒ r₁ + r₂ + r₃ = 12 cm    ----(4)

From (1), (2), (3) with (4) one by one we get

⇒ r₁ = 2 cm, r₂ = 6 cm, r₃ = 4 cm

Now, Area of sector with centre A (P) = (90°/360°) × π (r1)²  

⇒ (1/4) × π (2)² 

⇒ π, Hence condition 1 is correct 

Now, Area of sector with centre B (Q) = (θ/360)π (4)²

And  Area of sector with centre C (R) = [(90 - θ)/360]π (6)²

The value of  9Q + 4R = 9 × 16πθ /360 + 4 × 36(90 - θ)π/360

⇒ 9Q + 4R = 144π [ θ + 90 - θ]/360

⇒ 9Q + 4R = 36π cm² Hence condition 2 is also correct

∴ The option 3rd is correct.

Concept:

Pythagoras theorem: In a right-angled theorem,

Hypotenuse² = Base² + Perpendicular²

Where R is the Radius of a circle of centre O

• cos (90° - θ) = sin θ 
• sin²θ + cos²θ = 1
• cos 90° = 0

Calculation:

We have, AB = 15 cm, BC = 9 cm, AC = 12 cm

12² + 9² = 144 + 81 = 225 = 15²

Hence, Δ ABC is a right-angled triangle in which ∠C = 90°

As we know, ∠A + ∠B + ∠C = 180°

⇒ ∠A + ∠B = 90° (∵ ∠C = 90°)

⇒ ∠A = 90° - ∠B

Now, the required value

cos² A + cos² B + cos² C 

⇒ cos² A + cos² (90° - A) + cos² 90°  

⇒ cos2 A + sin2 A + 0 [∵ cos 90° = 0]

⇒ 1 + 0 [∵ sin²θ + cos²θ = 1]

∴  cos² A + cos² B + cos² C = 1

Concept:

Pythagoras theorem: In a right-angled theorem, 

Hypotenuse² = Base² + Perpendicular²

Where R is the Radius of a circle of centre O

• cos (90° - θ) = sin θ 
• sin²θ + cos²θ = 1
• cos 90° = 0

Calculation:

We have, AB = 15 cm, BC = 9 cm, AC = 12 cm

12² + 9² = 144 + 81 = 225 = 15²

Hence, Δ ABC is a right-angled triangle in which ∠C = 90°

As we know, ∠A + ∠B + ∠C = 180°

⇒ ∠A + ∠B = 90° (∵ ∠C = 90°)

⇒ ∠A = 90° - ∠B

Now, the required value

sin² A + sin² B + sin² C 

⇒ sin² A + sin² (90° - A) + sin² 90°  

⇒ sin² A + cos² A + 1[∵ sin 90° = 1]

⇒ 1 + 1 = 2 [∵ sin²θ + cos²θ = 1]

∴  sin2 A + sin2 B + sin2 C = 2

Concept:

Pythagoras theorem: In a right-angled theorem, 

Hypotenuse² = Base² + Perpendicular²

Where R is the Radius of a circle of centre O

Calculation:

We have, AB = 12 cm, BC = 9 cm, AC = 15 cm

12² + 9² = 144 + 81 = 225 = 15²

Hence, Δ ABC is a right-angled triangle in which ∠C = 90°

Using the above concept, the radius of the circle

OA = OB = OC = 15/2 = 7.5 cm

∴ The radius of the circle is 7.5 cm

(X + Y) = 100 – 20 – 15 – 10 = 55     ---- (1)

(2X + Y) = 100 – 4 – 8 – 4 = 84     ---- (2)

From (1) and (2):

X = 29 and Y = 26

Mean = ∑x_if_i/∑f_i = 3760/100 = 37.6

Concept used:

Pythagoras Theorem states,

Hypotenuse² = Base² + Perpendicular²

Calculation:

According to the given data, this diagram is drawn.

Let, v and p are the centers of semi-circle S1 and circle S respectively.

In ΔpvC, ∠ pCv = 90°

vp = Sum of the radius of S3 and S = (R + r)

pC = Radius of semi-circle S1 - Radius of circle S

⇒ DC - r = (2R - r) [∵ DC = AC]

So, vp² = pC² + Cm

⇒ (R + r)² = (2R - r)² + R²

⇒ R² + 2Rr + r² = 4R² - 4Rr + r² + R²

⇒ ⇒ R² + 2Rr + r² = 5R² - 4Rr + r² 

⇒ 5R² - 4Rr + r²  - R² - 2Rr - r² = 0

⇒ 4R² - 6Rr = 0

⇒ 4R² = 6Rr 

⇒ 2R = 3r

∴ Option 4 is the correct answer.