संयुक्त बंकन आघूर्ण (M) और ऐंठन आघूर्ण (T) के तहत व्यास D के एक शाफ्ट के लिए,

अधिकतम प्रमुख प्रतिबल 

न्यूनतम प्रमुख प्रतिबल 

As can be observed from the figure,

Both ends will develop anticlockwise resistive moment against the deformation.

Sway in the rigid frame can be predicted either by computing the moment of resistance or by analysis.

Method 1: Analysis by computing Moment of Resistance

There are two columns in the frame i.e. AB and CD

For the column AB ⇒ Moment of resistance against deformation =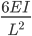 

For the column CD ⇒ Moment of resistance against deformation =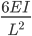 

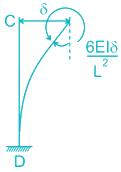
∵ Since both the columns have the same moment of resistance, the direction of sway cannot be predicted.

Method 2: Practical Analysis

Let’s divide the frame into two different portions, along the center line i.e. symmetrically.

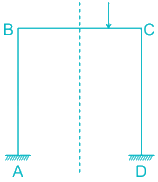
Since the left portion of the frame doesn’t carry any external load, it’s kept out of the analysis. Taking the right side of the frame.

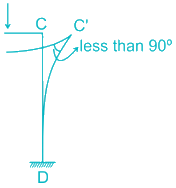
Assume Frame sways in the right direction,

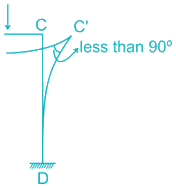
But right sway would lead the rigid joint to form an acute angle between the two members, which is not possible.

Now, assume sway in the left direction,

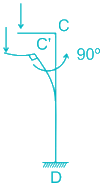
Yes, left sway would maintain the right angle between the two members.

As per Unwin’s Equation for calculating the minimum diameter of rivet for connecting members,

Stiffness Matrix Method

1. This method is also known as displacement method or equilibrium method.

2. It is suitable if static indeterminacy (D_s) > kinematic indeterminacy (D_k­) for the structure.

Stiffness is defined as Force required to produce unit displacement,

K₁₂ → Force at 2 due to unit displacement at 1

Flexibility Matrix Method

1. This method is also known as force method or compatibility method.

2. It is suitable if kinematic indeterminacy (D_k) > static indeterminacy (D_s) for the structure.

Flexibility is defined as Displacement caused due to unit Force.

δ₁₂ → Displacement at 2 due to Force at 1

Shear stress at any plane is given by,

For shear stress at a plane being zero, τ = 0

Yield loci for two yield criteria in-plane stress as per Von Mises and Tresca Criteria is given below:

As per IS 800 – 2007, rupture strength of the plate subjected to tensile loading is taken 90% of its ultimate strength.

Bolts connected to plates tend to redistribute moments along the width of the plate. Thus, a moment at a critical location is reduced and redistributed.

But to consider the factor of safety, for instance, if redistribution doesn’t occur ideally. IS Code has recommended taking rupture strength as 0.9 × f_u (f_u = ultimate strength of the material)

Degree of Redundancy is also known as static indeterminacy.

A structure is said to be statically indeterminate if the number of unknown forces of the given structure is more than the equilibrium equations available.

Static Indeterminacy (D_s­) = External static indeterminacy (D_se) + Internal static indeterminacy (D_si) – Number of Force Releases

D_se (External static indeterminacy) = Number of supports reactions – Number of equilibrium equation

∴ D_se (External static indeterminacy) = (2 + 3 + 1) – 3 = 3

D_si (Internal static indeterminacy) = 3 × C (for plane frame only)

Where C = Number of cuts required to open a closed configuration

D_si = 3 × 4 = 12

Force Release = m – 1 (for moment hinge only)

Where m = Number of members connected to a Moment hinge

In the above figure, a stone is thrown at an angle β from an inclined sloping ground of θ.

At the topmost vertical position, vertical component of velocity is zero.

A body is said to be in equilibrium if the net forces acting on a body is zero and body remains in its stable state i.e. no displacement.

Closure of Force Polygon ⇒ Vector sum of all the forces is zero.

Closure of Funicular Polygon ⇒ No displacement caused to the action of forces

Moment of inertia about an axis passing through its center, perpendicular to its plane is given by

Normal Stress on an inclined plane is given by,

Transverse Stiffeners are provided to increase buckling resistance of the web due to shear, It is provided vertically along the span.

Horizontal Stiffener / Longitudinal Stiffener is designed to prevent web buckling due to bending compression.

End Bearing Stiffeners are provided at the supports & Load Bearing Stiffeners are provided at the points of concentrated loads.

As per IS 800-1984 (Working Stress Method),

Shear lag factor (K) for

a) Single angle section connected to gusset plate by one leg only ⇒ K = 

b) Double angle connected back to back on the same side of gusset plate and tack riveted ⇒ K = 

As per IS 800:2007 (Limit State Method)

Shear lag factor is replaced by the reduction factor for calculating reduced tensile strength of the outstanding leg of tensile member given by,

`

Economical depth of Plate Girder as per Working Stress Method is given by

Note:

If the depth of girder is less than 750 mm, it is called shallow plate girder.

If the depth of girder is more than 750 mm, it is called deep plate girder.

μ₁ (coefficient of Static Friction) is effective when the body is at rest and motion of the body is completely opposed by the Frictional Force.

μ₂ (coefficient of kinetic friction) is effective when the body is in motion and its motion is opposed to some small fraction by Friction Force.

For the same cross-sectional area of the sections,

Note:

For three hinged arches subjected to temperature change, change in horizontal thrust with respect to temperature change is given by,

∴ x percentage increase in the height of arch would result in x percentage decrease in the horizontal thrust and vice versa.

Since the temperature is rising, the height of the arch will increase, and the horizontal thrust will decrease.

Member CG is a diagonal member in the given truss.

As a unit load moves along the truss AB,

All the members present in the bottom beam as such AF, FG, GH, and HB are subjected to pure tension and all the members present in the upside beam as such CD and DE are subjected to pure compression.

Member CG is a diagonal member where joint C is in compression and G is in tension.

⇒ The only diagram depicting the compression at C and tension at G is option D.

Note: Shortcut for calculating the value of ILD diagram

ILD Value of the ILD for member CG i.e. diagonal members of any truss is given by

Where α → angle of inclination of a diagonal member w.r.t horizontal beam

a → Horizontal distance of the location of a particular pin joint considered

For converting real beam to conjugate beam,

As the beam is hinged at a distance of 3 meters from the support A, Let’s break the beam into two distinguished cantilever beams with load ‘X’ and ’20 – X’ respectively.

Deflection for the hinged point would be equal for both of cantilever beam as shown in figure

Deflection of the hinged end from cantilever Beam A = Deflection of the hinged end from cantilever Beam B

This option is directly eliminated, it signifies higher shear at support A as compared to support B, which is completely wrong.

This option is directly eliminated, it signifies higher shear at support A as compared to support B, which is completely wrong.

∴ For gravity loading → Slope of the Shear Force Diagram should increase with the increasing intensity of loading.

SFD in the above option shows decreasing slope value of SFD for increasing load intensity which is wrong.

∴ The above SFD is correct.

Allowable axial compressive stress

The allowable compressive stress is inversely proportional to the square of slenderness ratio.

This shows a linear relationship between compressive strength and slenderness ratio which is wrong.

This also shows a linear relationship between compressive strength and slenderness ratio which is wrong.

This shows a finite compressive strength for zero slenderness ratio value, practically zero value of slenderness ratio is not possible and even if it’s possible, compressive strength should be infinite.

All of the above mentioned are the different method to compute deflection of a truss joint.

Reduction for the welded joint is considered only if,

if the angle of fusion is 60°to 90° or if the angle of fusion is not given.

Length of joint is 700 mm > 630 mm (150 × 4.2)

Point of Contraflexure ⇒ Point where the bending moment changes its sign is termed as a point of contraflexure.

For the given frame,

Fixed End Moment Direction is given by

Therefore Fixed Moment Diagram is given by

Assuming all beams to be simply supported, Bending Moment diagram is given as

Now overlapping two diagrams,

Joint O is connected to the four-member OA, OB, OC, and OD where far end is supported by vertical guided roller, vertical roller support, fixed support, and horizontal roller support respectively.

Stiffness for OA is 

Stiffness for OB is 0

Stiffness for OC is 

Stiffness for OD is 

∴ Stiffness for joint O is the sum of the stiffness for all the members connected to it.

Stiffness for the joint O is