Given:

f: R→ R such that f(x + y) = f(x).f(y) for all x, y ∈ R and f(x) ≠ 0.

f(x) is differentiable at x = 0 and f'(0) = 2

f'(x) = λ. f(x)

Calculation:

Putting x = y = 0 in f(x + y) = f(x).f(y)

f(0) = [f(0)]²

⇒ f(0)[1 - f(0)] = 0

⇒ f(0) = 1 as f(x) ≠ 0

Also, f'(x) = λ. f(x)

Putting x = 0, we get f'(0) = λ. f(0)

⇒ λ = 2

Calculation 

Let assume the class interval and frequency table for this histogram to solve this question

Histogram for this data

Average = Σfx/Σf

⇒ Average = 1145/35 = 32.7

Range:

In case of continuous frequency distribution, range, is calculated as the difference between the lower limit of the minimum interval and upper limit of the maximum interval of the grouped data. That is for X:  0-10, 10-20, 20-30 up to 60-70, range is calculated as 70 - 0 = 70.

∴ The range of frequency is above average

Concept:

Cube roots of Unity

Cube roots of unity are given by 1, ω, ω², where

Some Results Involving Complex Cube Root of Unity (ω)

(i) ω³ = 1

(ii) 1 + ω + ω² = 0

(iv) ω̅  = ω2

Calculation:

Statement I: roots are -2, 1 - 3ω, 1 - 3ω2

(z -1)³ = - 27

⇒ (z -1) = (- 27)^1/3 

⇒ (z -1) = - 3 ⋅ (1)^1/3 

⇒ z  =  - 3 ⋅ (1) ^1/3  + 1

⇒ z  =  1 - 3 ⋅ (1) ^1/3 

Cube root of unity are 1, ω, ω²

For 1, z  =  1 - 3 ⋅ 1 ⇒ z  =  1 - 3 =  - 2

For ω, z  =  1 - 3 ⋅ ω ⇒ z  =  1 - 3ω 

For ω², z  =  1 - 3 ⋅ ω² ⇒ z  =  1 - 3ω² 

Statement I is correct.

Statement II: Sum of roots is 0

Roots of the equations (z -1)3 + 27 = 0 are - 2, 1 - 3ω, 1 - 3ω2 

Sum of roots = (- 2) + (1 - 3ω) + (1 - 3ω2) 

= - 3ω - 3ω2 ⇒ - 3(ω + ω2) = -3(-1) = 3

Statement II is incorrect.

Statement III: Product of roots is 1

Product of roots = (-2) (1 - 3ω)(1 - 3ω2)

= (-2) (1 - 3ω² - 3ω + 9ω³)

= (-2)(10 - 3(ω2 + ω))

= (-2)(10 + 3)

= -26

Statement III is correct.

∴ I and III are correct.

Concept:

Concept:

For a real polynomial, complex roots occur in conjugate pairs,

that is, if x + iy is the root of a polynomial then x - iy is also the root of that polynomial.

If α and β are the roots of the equation ax2 + bx + c = 0,

Calculation:

Let z = x + iy

and given Re z = 1 ⇒ x = 1

So, the roots of the equation z² + γz + δ = 0 are 1 + iy and 1 - iy

∵ Product of roots → (1 + iy)(1 - iy) = α β  = δ 

⇒ Product of roots → (1 + iy)(1 - iy) = δ

⇒ δ = 1 + y² ≥ 1

So, δ ϵ [1, ∞)

∴ The correct answer is option (4).

Given:

Coins are numbered 1 to 10.

The drawn coin has a number more than 3.

Concept:

An even number is a number that is divisible by 2.

Formula:

Calculation:

Let A be the event that number is even and B be the event that number is more than 3.

Numbers that are even and more than 3 are ' 4, 6, 8, 10 ' 

∴ P(A ∩ B) = 4/10   -----    (i)

Numbers more than 3 are ' 4, 5, 6, 7, 8, 9, 10 '

and P(B) = 7/10    -----   (ii)

Dividing (i) by (ii) -

∴ P(A/B) = 4/7

Concept:

Calculation:

Formula used:

1. Midpoint of coordinates (x₁, y₁) & (x₂, y₂)

2. The equation of passing through (x₁, y₁) and slope m is

y - y₁ = m(x - x₁)

3. If the slope of two perpendicular lines is m₁ & m₂ then

m₁ × m₂ = -1

Calculation:

Let slope of the projection line (L) is m.

We know that line joining the PQ will be perpendicular to line L.

The slope of line PQ × Slope of line L = -1

Concept:

Conditional probability: It is the measure of probability of an event A is occurring given that another event B is already occurred, then:

Calculation:

Given: Box1: 4W + 3B & Box2: 3W + 4B

Probability of black ball from box1 = 3/7

Probability of black ball from box2 = 4/7

Probability of choosing first box = 3/6 = 1/2

Probability of choosing second box = 3/6 = 1/2

Probability of choosing black ball = (Probability of choosing the first bag × Probability of choosing black) + (Probability of choosing the second bag × Probability of choosing black)

Concept:

1) The equation of a plane passing through a point P (x1, y1, z1) is given by:

a (x - x₁) + b (y - y₁) + c (z - z₁) = 0 where a, b, c are constants.

2) If the angle between the lines 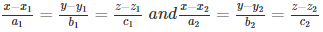 where a₁, b₁, c₁, a₂, b₂ and c₂ are the direction ratios is 90° then

a₁ ⋅ a₂ + b₁ ⋅ b₂ + c₁ ⋅ c₂ = 0

Calculation:

Given:

Plane passes through (4, 6, 2) and (4, - 5, 3) and is parallel to the x - axis.

As we know that the equation of a plane passing through a point P (x₁, y₁, z₁) is given by: a (x - x₁) + b (y - y₁) + c (z - z₁) = 0

So, the equation of plane passing through the point (4, 6, 2) is given by:

⇒ a (x - 4) + b (y - 6) + c (z - 2) = 0       ----(1)

It is given that plane also passes through the point (4, - 5, 3) i.e the point (4, - 5, 3) will satisfy the equation (1)

⇒ a (4 - 4) + b (- 5 - 6) + c (3 - 2) = 0

⇒ - 11b + c = 0       ----(2)

Also it is given that plane represented by (1) is parallel to the x - axis i.e the normal to the plane represented by (1) is perpendicular to the x - axis

The direction ratios of the normal to the plane represented by (1) are: a, b, c

Similarly, the direction ratios of the x - axis are: 1, 0, 0

As we know that if two lines are perpendicular then a₁a₂ + b₁b₂ + c₁c₂ = 0 where a₁, b₁, c₁, a₂, b₂ and c₂ are the direction ratios

⇒ a ⋅ 1 + b ⋅ 0 + c ⋅ 0 = 0

⇒ a = 0

Let b = k then c = 11k

By substituting a = 0, b = k and c = 11k in equation (1), we get

⇒ 0 ⋅ (x - 4) + k (y - 6) + 11k (z - 2) = 0

⇒ y + 11z – 28 = 0

Hence, the equation of the required plane is: y + 11z – 28 = 0