Given:

Average of 7 numbers: 158

Calculation:

⇒ Sum of the 7 numbers = Average × Total numbers

⇒ Sum of the 7 numbers = 158 × 7 = 1106

⇒ Number deleted = Sum of the 7 numbers - Average × (Total numbers - 1)

⇒ Number deleted = 1106 - 158 × 6

⇒ Number deleted = 1106 - 948

⇒ Number deleted = 158

Therefore, the deleted number is 158.

Given:

Total profit = Rs. 800000

Taxes = 25%

A : B = 5 : 1

Calculation:

⇒ Tax paid = 800000 × 25/100 = Rs. 200000

⇒ Remaining profit = Rs. (800000 – 200000) = Rs. 600000

The remaining profit is divided among A and B in the ratio 5 ∶ 1

Suppose, Share of A = 5x and

Share of B = x

According to the question,

5x + x = 600000

⇒ x = 100000

∴ Share of A = 5 × 100000 = Rs. 500000

∴ Share of B = 1 × 100000 = Rs. 100000

Given:

Aarav spends on food = 40% of his income.

Deposits money for health insurance = 1/5 of the remaining income.

Saving of Aarav per month Rs. 4800 equals to 1/2 of the balance.

Formula used:

Income = Expenditure + Saving

Calculation:

Let the total salary of Aarav be 100x

Total expenses on food = 40% × 100x = 40x

Remaining salary = 100x - 40x = 60x

Now, Total deposits on bank  = 1/5 of balance = (1/5 × 60x) = 12x

Then, Aarav's monthly savings is Rs 4800 = 1/2 of the remaining balance.

Therefore,

1/2 of the remaining balance = 1/2 × (60x - 12x) = 1/2 × 48x = 24x

According to the question

⇒ 24x = 4800

⇒ x = 4800/24 = 200

So, monthly salary is 100x = 100 × 200 = 20,000

∴ Aarav's monthly salary is Rs. 20,000.

Given:

A certain sum at certain rate % per annum simple interest becomes 2100 in 2 years and 2250 in 5 years.

Formula Used:

S.I = P × r × t/100; A = P + S.I, where P = principal, r = rate p.a., t = time period, A = amount

Calculation:

Let the principal sum and rate of interest be 'P' and r% p.a. respectively

Since the simple interest remains the same for each year for a given principal and rate p.a.

⇒ A₅ = P + S.I for 5 years    ......(i)

also A₂ = P + S.I for 2 years     ......(ii)

on subtracting equation (ii) from equation (i). we get 

⇒ 2250 - 2100 = S.I for 3 years

⇒ 150 = S.I for 3 years

⇒ S.I for 1 years = 150/3 = 50

⇒ A₂ = P + S.I for 2 years

⇒ 2100 = P + 50 × 2

⇒ P = 2000

also, 50 = 2000 × r × 1/100

⇒ r = 2.5% p.a

∴ required principal and rate of interest are 2000 and 2.5% p.a. respectively

Let, Speed of the stream = x km/hr

Given,

It takes twice the time to row upstream than the time to downstream

Let time taken downstream be k hr, then time taken in upstream must be 2k hr

As, Distance = time × speed

Given:

A sum doubles itself in 6 years on simple interest. The difference between the compound interest and the simple interest earned on that certain amount at same interest rate in 2 years is Rs. 480

Formula used:

Difference between CI and SI for 2 years = CI – SI = x × (r/100)²

Calculation:

Let sum be x, so amount be 2x

⇒ Amount = Principal + Interest

⇒ 2x = x + (x × r × 6)/100

⇒ r = 100/6 = 16.66%

Also, difference between CI and SI on that certain sum for 2 years is Rs. 480

⇒ CI – SI = x × (r/100)²

⇒ 480 = [x × (100/6)²]/100²

⇒ x = Rs. 17280

∴ required sum = Rs. 17280

Given:

Speed of farmer going to the market (s) = 9 km/hr.

Speed of farmer returning from the market (s') = 8 km/hr.

Total time taken for the whole journey = 1 hour 42 minutes =  hours = (102 / 60) hours.

Formula used:

Speed = distance / time.

Calculation:

Let the total distance be x km.

Speed = distance / time

Time = distance / speed

x = 102 × 72 / 60 × 17

x = 72 / 10

x = 7.2 km.

∴ The total distance of market from his village is 7.2 km.

Given:

Two persons 24 km apart start at the same time and are together in 8 hrs if they walk in same direction.

They walk in opposite direction, they are together in 4 hrs. 

Concept used:

In same direction, the speed is subtracted i.e. (a – b)

In opposite direction, the speed is added i.e. (a + b)

Calculation:

Let a = the walking rate of the 1st person which is the fastest walker

let b = the walking rate of the 2nd person

Now,

⇒ 8(a – b) = 24 ....(1)   [Walking in the same direction]

⇒ 4(a + b) = 24 ....(2)   [Walking in the opposite direction]

Simplifying the equations, we get

⇒ (a – b) = 3 ....(3)

⇒ (a + b) = 6 ...(4)

Now, solving the equations we get

⇒ 2a = 9

⇒ a = 4.5

Putting the value of a in equation (4), we get

⇒ (4.5 + b) = 6

⇒ b = (6 – 4.5)

⇒ b = 1.5

∴ The required speeds is 4.5km/hr and 1.5 km/hr.

Given:

P = 1500 Rs

T = 3 years 

Difference = 13.50 Rs

Formula used:

Simple interest = (P× R × T)/100

Here, P = Principal, R = Rate, T = Time

Calculation:

Let r₁ and r₂ be the required rate of interest.

Then,

⇒13.50 = [(1500 × 3 × r₁)/100] - [(1500 × 3 × r₂)/100]

⇒ 13.50 = 4500/100(r₁ - r₂)

⇒ r₁ - r₂ = 135/450

⇒ r₁ -r₂ = 27/90 

⇒ r₁ -r₂ =  3/10 =  0.3

∴ The difference between their rates of interest is 0.3%

Given,

Four vessels are filled with mixture of wine, water and cold drink with wine concentration 20%, 30%, 40% and 70% respectively.

Formula:

Mixture and Allegation method:

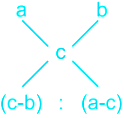
Where, a > c > b

Calculation:

Let concentration of wine in first two vessels emptied into another vessel be x, then

Using allegation method

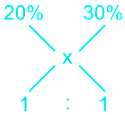
According formula

(30 – x)/(x – 20) = 1/1

⇒ 30 – x = x – 20

⇒ x + x = 30 + 20

⇒ 2x = 50

⇒ x = 50/2

∴ x = 25%

Similarly,

Let concentration of wine in last two vessels emptied into another vessel be x, then

Using allegation method

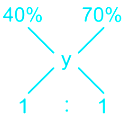
According formula

(70 – y)/(y – 40) = 1/1

⇒ 70 – y = y – 40

⇒ y + y = 70 + 40

⇒ y = 110

⇒ y = 110/2

∴ y = 55%

If 25% and 55% concentration of wine of two vessels emptied into a large vessel,

Let concentration of wine in large vessel be z%, then

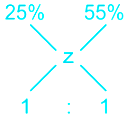
According formula

(55 – z)/(z – 25) = 1/1

⇒ 55 – z = z – 25

⇒ z + z = 55 + 25

⇒ 2z = 80

⇒ z = 80/2

∴ z = 40%

Alternate Method

Let capacity of each vessel be 100x

Hence, wine in respective vessels = 20x, 30x, 40x and 70x.

And, total amount = 4 × 100x = 400x

∴ Required concentration = [(20x + 30x + 40x + 70x)/400x] × 100 = (160x/400x) × 100) = 40%