Calculation:

⇒ Total population of all the villages = 60000

⇒ Population of village D = 60000 × 17/100 = 10200

⇒ Population of village E= 60000 × 18/100 = 10800

⇒ Difference between the population of village D & E = 10800 – 10200 = 600

Therefore, the difference between the population of village D & E is 600.

Given:

ZX(hypotenuse) = 9√3 cm

We know that, cosθ = base/hypotenuse

⇒ cos60° = YZ/ZX

⇒ 1/2 = YZ/9√3

∴ YZ = 9√3/2 cm

Given:

So, they do the total work  in  (24 / 5 ) × 5 = 24 days

 A + B together 1 day's work = 1 / 24

Again,

A  alone completes 3/4 of the work in 30 days.

So, A does the total work  in  30 × (4 / 3 )  = 40 days

A's 1 day's work will be = 1 / 40

B's 1 day's work will be = (1 /24) - (1 / 40)

⇒ 2 /120

⇒ 1 / 60

∴ B can do the whole work in 60 days.

Alternate Method

Calculation:

So, they do the total work  in  (24 / 5 ) × 5 = 24 days

Again,

A  alone completes 3/4 of the work in 30 days.

So, A does the total work  in  30 × (4 / 3 )  = 40 days

Let total work be 120 units ( LCM of 24 and 40)

So, the efficiency of A + B = 120 / 24

⇒ 5  units

Efficiency of A = 120 / 40

⇒ 3  units

Efficiency of B = 5 - 3

⇒ 2 units

Total work = 120 units 

Time taken to complete total work by B 

⇒ 120/2 = 60 days

∴ B can do the whole work in 60 days.

Concept used:

Calculation:

325 + 276 ÷ [150 − {9 × 9 + (83 − 4 × 15)}]

⇒ 325 + 276 ÷ [150 − {9 × 9 + 23}]

⇒ 325 + 276 ÷ [150 − 104]

⇒ 325 + 276 ÷ 46

⇒ 325 + 6 = 331

Given:

Four friends A, B, C and D made investments in a business in the ratio 3 ∶ 7 ∶ 9 ∶ 13, respectively. 

The share of the profit of C is Rs. 8,910.

Concept used:

Profit is shared in the ratio of the investment of partners.

Calculation:

Let the total profit be P.

According to the question,

P × 9/(3 + 7 + 9 + 13) = 8910

⇒ P = (8910 × 32)/9 = 31,680

Now, the total share of the profits of A and B

∴ The total share of the profits of A and B is Rs. 9,900.

Given:

The income of A = 30% less than the income of B

The income of B = 137.5% more than that of C

Income of A = Rs. 28500 less than that of B

Calculation:

Let the income of A be Rs. A, B be Rs. B and C be Rs. C respectively

Income of B is 137.5% more than that of C 

⇒ B = C × (100 + 137.5)/100

⇒ B = C × (2375/1000)

⇒ B = Rs. 19C/8 ......(1)

Income of A is 30% less than the income of B

⇒ A = B × (100 – 30)/100

⇒ A = B × 70/100

Substituting the value of B in equation (1)

⇒ A = (19C/8) × 7/10

⇒ A = 133C/80 .......(2)

Difference between B's income and A's income = Rs. 28500

⇒ B – A = 28500

Substituting the values of A and B from equation (1) and (2)

⇒ 19C/8 – 133C/80 = 28500

⇒ (190C – 133C)/80 = 28500

⇒ 57C/80 = 28500

⇒ C = (28500 × 80)/57

⇒ C = 500 × 80

⇒ C = Rs. 40000

∴ The income of C is Rs. 40000

Alternate Method

137.5% = 100% + 37.5% = 1 + 3/8 = 11/8

Let income of C be 8

Then, income of B = 19

Income of A is 30% less than the income of B,

⇒30/100 × 19 = 5.7

Thus, Income of A = 19 - 5.7 = 13.3

Difference of incomes of A and B = 5.7

Actual Difference = 28500

5.7-----------28500

1-----------5000

∴ Income of C = 5000 × 8 = Rs. 40,000

Let cost price of the article be Rs. x, then

According to the question

120x/100 – 116x/100 = 36

⇒ (120x – 116x)/100 = 36

⇒ 4x/100 = 36

∴ x = 900

Short Trick:

Let cost price of the article be 100%

20% - 16% = 36

⇒ 4% = 36

⇒ 1% = 9

∴ 100% = 900

Given:

The set of numbers is 30, 45, 150.

Formula:

Highest Common Factor (HCF) is the largest number that divides each of the given numbers.

Calculation:

The factors of 30 are 1, 2, 3, 5, 10, 15, 30.

The factors of 45 are 1, 3, 5, 9, 15, 45.

The factors of 150 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150.

The common factors of 30, 45, and 150 are 1, 3, 5, 15.

HCF = 15

Therefore, the HCF of the numbers 30, 45, and 150 is 15.

Let the radii of the spherical balls be r cm and r/2 cm.

Radius of the cylinder R = 18/2 = 9 cm.

According to the question

(4/3) π [r³ + (r/2)³] = π R² h

⇒ (4/3) [r³ + r³/8] = 9 × 9 × 4

⇒ 9r³/8 = 9 × 9 × 3

⇒ r³ = 9 × 3 × 8

⇒ r = ∛[3 × 3 × 3 × 2 × 2 × 2]

⇒ r = 3 × 2

⇒ r = 6 cm

⇒ r/2 = 3 cm

So, radii of the cylinder are 3 cm and 6 cm.

Alternate Method

Shortcut Trick

Let, time taken by B = t hours and, A = t + 2

Now, the speed of B = 40/t kmph and the speed of A = 40/(t + 2) kmph

We know, Distance = Speed × time

To travel a distance of 80 km A doubles his speed

Time taken by A to cover  40 km distance = t + 2 hours, where t is the time taken by B to cover the distance.

Time taken by A to cover the 40 km distance when its speed is double = Time taken to cover 80 km distance/2 = (2t + 3/2)/2 = t + 3/4

Distance = (S₁ × S₂)/(S₁ - S₂) [Time difference]

Here, S₁ = x, S₂ = 2x (For A)

40 = 2x × x/(2x - x)[t + 2 - t - 3/4]

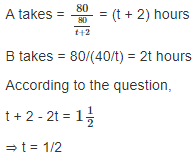
Now B takes 1/2 hours to cover 40 km

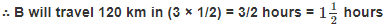
⇒ 40 = 2x(5/4)

⇒ x = 16

Actual time taken by A = 40/16 = 2.5 hours

Actual time taken by B = 2.5 -  2 = 0.5 hour

Speed of B = 40/0.5 = 80 km/h

Required time taken by B = 120/80 = 3/2 hours

Traditional method:

Given:

A takes 2 hours more than B to cover a distance of 40 km

When A doubles his speed, he takes 1.5 hours more than B to travel 80 km

Concept used:

Distance = Speed × Time

Calculation:

Let The speed B be x km/h.

Time taken by B to cover 40km = 40/x hour

Time taken by A to cover 40km = [(40/x) + 2] hour

Speed of A = (40)/[(40 + 2)/x] kmph

⇒ (20x)/(20 + x) kmph ……… (1)

Now,

Time taken by B to cover 80 km = 80/x hour

When A doubles his speed = (40x)/(20 + x) kmph

Time taken by A to cover 80 km = 80/(40x)/(20 + x)

⇒ (40 + 2x)/x hour

Now in this case,

A takes 1.5 hour more than B to travel 80 km

So,

⇒ (40 + 2x)/x - 80/x = 3/2

⇒ (40 + 2x - 80)/x = 3/2

⇒ 4x - 80 = 3x

⇒ x = 80

So,

Speed of B is 80 kmph.

Now,

To cover a distance of 120 km, B will take

⇒ 120/80 = 1.5 hours

∴ To cover a distance of 120 km, B will take 1.5 hours.