Please wait...

Time Work & Wages Test 458
Result
Time Work & Wages Test 458

  • /

    Score

  • -

    Rank
Time Taken: -
  • Question 1/10
    1 / -0.25
    A, B and C can do a piece of work in 30 days, 40 days and 50 days, respectively. Beginning with A, if A, B and C do the work alternatively then in how many days will the work be finished?
    Solutions
    A, B and C can do a piece of work in 30 days, 40 days and 50 days, respectively.

    ∴ Total work = LCM of 30, 40 and 50 = 600 units

    Efficiency of A = 600/30 = 20

    Efficiency of B = 600/40 = 15

    Efficiency of C = 600/50 = 12

    Since, they work on alternate days starting with A, therefore work done by A, B and C on first, second and third day respectively are 20 units, 15 units and 12 units.

    3 days → 47 units

    ∴ 36 days → 564 units

    Work done by A on 37th day = 20 units

    And, work done by B on 38th day = 15 units

    Remaining work = 600 – 564 – 20 – 15 = 1 unit

    Time taken by C to do a remaining work = 1/12

    ∴ Total time = 38 + 1/12 = 38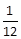days

    Hence, option A is the correct answer.

  • Question 2/10
    1 / -0.25
    A is thrice as good a workman as B and together they can finish a work in 32 days. In how many days will B alone complete the same work?
    Solutions
     A is thrice as good a workman as B and together they can finish a work in 32 days.

    ∴ Ratio of efficiency:

    A : B = 3 : 1

    And, total work = (3+1)32 = 128 units

    ∴ Time taken by B alone to complete the work

    = 128/1 = 128 days

    Hence, option D is the correct answer.

  • Question 3/10
    1 / -0.25
    A, B and C can all together do a piece of work in 10 days, in which B takes 3 times as long as A and C together to do the work. In how many days can B alone do the work?
    Solutions

    Efficiency of B and (A + C) = 1 : 3

    Total efficiency of A, B and C = 1 + 3 = 4 units

    Total work = Efficiency × Time

    = 4 × 10 = 40 units

    Time taken by B to complete the work = 40/1 = 40 days

  • Question 4/10
    1 / -0.25
    A can do a work in 10 days and B can do the same work in 15 days. If they work on it together for 4 days, then the fraction of the work that is left is:
    Solutions

    Let the total work be 30 units (LCM of 10 and 15).

    Efficiency of A = 30/10 = 3 units/day

    Efficiency of B = 30/15 = 2 units/day

    4 days work of A and B = 4(3+2) = 20 units

    Remaining work = 30 – 20 = 10 units

    Required fraction = 10/30 = 1/3

  • Question 5/10
    1 / -0.25
    In one-sixth of the time that B takes to complete a piece of work, A can complete half of the same work. If working together they take 16 days to complete the work, how much time shall B take to complete it alone?
    Solutions

    Time ratio for A & B to complete whole work = 1 : 6/2 = 1 : 3

    Efficiency ratio A : B = 3 : 1

    Time for B to work alone = (3+1)×16/1 = 64 days

  • Question 6/10
    1 / -0.25
    15 persons begin to work together on a job, but after some days 6 persons leave. As a result, the job which could have been completed in 42 days is completed in 54 days. After how many days of the commencement of the work did 6 persons leave?
    Solutions

    Let 6 persons leave after x days.

    Then, 15 × 42 = 15x + 9(54 – x)

    ⇒ 630 = 15x + 486 – 9x

    ⇒ 6x = 630 – 486 = 144

    ⇒ x = 24

    Hence, the correct answer is option A.

  • Question 7/10
    1 / -0.25
    If 20 men can complete a work in 48 days, then how many men should be employed to complete the same work in 40 days?
    Solutions

    We know that

    men

  • Question 8/10
    1 / -0.25
    32 workers working for 9 hours a day can finish a work in 14 days. If each worker works for 8 hours per day, how many workers are required to finish the same work in 18 days?
    Solutions

    Let the x workers can finish the work in 18 days.

    By MDH formula:

    32 × 9 × 14 = x × 8 × 18

    ⇒ x = 28

  • Question 9/10
    1 / -0.25
    A and B undertake to do a job for Rs. 6,000 . A can do it in 10 days and B do it in 12 days. With the assistance of C, they finish the work in 4 days. How much should C be paid for his work?
    Solutions

    Total work = LCM of 10, 12 and 4 = 60 units

    Efficiency of A = 60/10 = 6

    Efficiency of B = 60/12 = 5

    Efficiency of A+B+C = 60/4 = 15

    ∴ Efficiency of C = 15 – 6 – 5 = 4

    ∴ C should be paid = [6000/15] × 4 = Rs 1600

  • Question 10/10
    1 / -0.25
    A, B and C can complete a piece of work in 60, 30 and 20 days respectively. In how many days can A complete the work if he is assisted by B and C together on every fifth day.
    Solutions
    Total work = LCM of 60, 30 and 20 = 60 units

    Efficiency of A = 60/60 = 1

    Efficiency of B = 60/30 = 2

    Efficiency of C = 60/20 = 3

    Now, work done by A in first four days = 4 × 1 = 4 units

    Work done by A, B and C together on fifth days

    = 1 + 2 + 3 = 6 units

    ∴ 5 days → 10 units

    ⇒ 30 days → 60 units

    ∴ Work is completed in 30 days.

User Profile
-

Correct (-)

Wrong (-)

Skipped (-)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
Get latest Exam Updates
& Study Material Alerts!
No, Thanks
Click on Allow to receive notifications
×
Open Now