CONCEPT:

• The ac circuit containing the capacitor, resistor, and inductor is called an LCR circuit.
• For a series LCR circuit, the total potential difference of the circuit is given by:

$V=\sqrt{V_R^2+{\left(V_L-V_C\right)}^2}$

Where VR = potential difference across R, VL =  potential difference across L and VC =  potential difference across C

• For a series LCR circuit, Impedance (Z) of the circuit is given by:

$$$Z=\sqrt{R^2+{\left(X_L-X_C\right)}^2}$
Where R = resistance, XL =induvtive reactance and XC = capacitive reactive

EXPLANATION :

• Resonance of an LCR circuit is the frequency at which capacitive reactance is equal to the inductive reactance, X_c = X_L, then the value of impedance is given by

$\Rightarrow Z=\sqrt{R^2+{\left(X_L-X_C\right)}^2}$

$\Rightarrow Z=\sqrt{R^2+0}$

$\Rightarrow Z=R$

• At resonance, the value of impedance is purely resistive. Hence, option 1 is the answer

The correct answer is option 4) i.e. 4 A

CONCEPT:

• Peak value: The maximum value attained by the alternating current during a cycle is called its peak value. Considering alternating current as a sinusoidal wave, the peak value is its amplitude or crest value. 

• RMS value: RMS current is that value of steady current which when flowing through a given resistance for a given period of time, produces the same quantity of heat like that of an alternating current flowing through the same resistance and for same time period.
  • It is also known as the effective value of alternating current.

The RMS current I_rms is related to the peak current I₀ as:

 $I_{rms}=\frac{I_0}{\surd 2}$

CALCULATION:

Given that:

​The peak value of current, I₀ = 4√2

RMS value of current, $I_{rms}=\frac{I_0}{\surd 2}=\frac{4\sqrt{2}}{\surd 2}=$ 4 A

Concept:

For an RLC circuit, the power factor is given as cosine of phase angle

i.e., $cos\varphi =\frac{R}{Z}$

Here, R is resistance and Z is the impedance of RLC combination if the amount of current is i = im sin(ωt + φ) and v = vmsinωt

Where,

i, v = RMS value of current  and voltage respectively 

φ = Phase angle

ω = angular frequency 

i_m, v_m = maximum value of current and voltage 

Explanation:

From the above explanation, we can see that for an RLC combination the power factor is given as 

$cos\varphi =\frac{R}{Z}$

Hence option 3 is correct among all

CONCEPT:

• The ac circuit containing the capacitor, resistor, and inductor is called an LCR circuit.
• For a series LCR circuit, the total potential difference of the circuit is given by:

$V=\sqrt{V_R^2+{\left(V_L-V_C\right)}^2}$

Where VR = potential difference across R, VL =  potential difference across L and VC =  potential difference across C

• For a series LCR circuit, Impedance (Z) of the circuit is given by:

$$$Z=\sqrt{R^2+{\left(X_L-X_C\right)}^2}$
Where R = resistance, XL =induvtive reactance and XC = capacitive reactive

• The resonant frequency of a series LCR circuit is given by

$\Rightarrow \nu =\frac{1}{2\pi \sqrt{LC}}$

CALCULATION:

As we know that,

Inductive Reactance (X_L) = ωL

• Given alternating voltage

⇒ V = 200 sin 100 πt

Comparing with standard voltage equation

⇒ V = V_m sin ωt

We get,

⇒ ω = 100π

Now, inductive reactance 

$\Rightarrow X_L=100\pi \times \frac{2}{\pi }$

⇒ X_L = 200 Ω

• Capacitive reactance 

$\Rightarrow X_C=\frac{1}{\omega C}$

$\Rightarrow X_c=\frac{1}{100\pi \times \frac{100}{\pi }}\times {10}^6$

⇒ Capacitive reactance (X_c) = 100 Ω

• The impedance of the circuit is given by

$\Rightarrow Z=\sqrt{R^2+{\left(X_L-X_C\right)}^2}$

$\Rightarrow Z=\sqrt{{100}^2+{\left(200-100\right)}^2}$

$\Rightarrow Z=\sqrt{10000+10000}$ $=\sqrt{{10}^4+{10}^4}$ $=\sqrt{2\times {10}^4}$

$\Rightarrow Z=100\sqrt{2}$ = 100 × 1.414 = 141.4 Ω

CONCEPT:

• Wattless current: The current in AC circuit is said to be wattless current if the average power consumed in such circuit corresponds to zero and such current is also called idle current. 

The average power of an AC circuit is given by:

Pav = ErmsIrms cos ϕ

The current Irms can be resolved into two components i.e. along with parallel and perpendicular components.

• The Component Irms cosϕ is along Erms . Here the phase angle between Irms cosϕ and Erms is zero.

Pav = Erms (Irms cos ϕ) cos 0 =  Erms Irms cos ϕ

• The Component Irms sinϕ is normal to Erms . Here the phase angle between Irms sinϕ and Erms is π/2.

Pav = Erms (Irms sin ϕ) $\cos \frac{\pi }{2}$ = 0

• We call the component Irms sin ϕ as the idle or wattles current because it does not consume any power in a.c. circuit.

EXPLANATION:

• Component Irms sinϕ is normal to Erms . As the phase angle between Irms sinϕ and Erms is π/2.

Pav = Erms (Irms sin ϕ) $\cos \frac{\pi }{2}$ = 0

• We call the component Irms sin ϕ as the idle or wattles current because it does not consume any power in a.c. circuit. This happens in a purely inductive or capacitive circuit in which current and voltage differ by a phase difference of π /2.
• Hence option 2 is correct.

NOTE:

• The wattless current is possible in a circuit where resistance is zero.

CONCEPT:

• Alternating current: The electric current whose direction changes periodically is called electric current.

• Frequency (ν): The number of waves that pass a given point per second is called frequency.
  • The unit of frequency is vibration per second or Hertz.

• Time period (T): The time taken to complete one full oscillation or cycle by the Wave is called time period.

  • The SI unit of the time period is second (s).

The relationship between time period and frequency is given as:

Time period (T) = 1/ν 

EXPLANATION:

Given that:

Frequency (ν) = 50 Hz

Time period (T) = 1/ν = 1/50 sec

So the time taken to complete one oscillation = 1/50 sec

Since this time is time for one complete oscillation, but the current changes its direction at midpoints (half-wave) itself. 

So time for reverse the direction = T/2 = 1/100 sec

Hence option 2 is correct.

Concept:

• Transformer: An electrical device that is used to transfer electrical energy from one electrical circuit to another is called a transformer.
  • In a transformer, there are two coils- The primary coil (P) and secondary coil (S).

There are two types of transformer:

• Step-up transformer: The transformer which increases the potential is called a step-up transformer.
  • The number of turns in the secondary coil is more than that in the primary coil.
• Step-down transformer: The transformer which decreases the potential is called a step-down transformer.
  • The number of turns in the secondary coil is less than that in the primary coil

In a transformer, the voltage in secondary is calculated by:

 $\frac{N_s}{N_p}=\frac{V_s}{V_p}=\frac{I_p}{I_s}$

Here, Np and Ns are the numbers of turns in the primary and the secondary coils respectively and Vp and Vs are the RMS voltages across the primary and secondary respectively and I_p and I_s are primary and secondary currents.

Calculation:

Given that:

The ratio of turns of coil N_p / N_s = 1 / 20

We know that

$\frac{N_s}{N_p}=\frac{I_p}{I_s}$

$\Rightarrow \frac{20}{1}=\frac{I_p}{I_s}$

⇒ I_P : I_s = 20 : 1

CONCEPT:

AC Generator:

• An AC generator is a device that converts mechanical energy into electrical energy and generates alternating current.
• It works on the principle of electromagnetic induction i.e., when a coil is rotated in a uniform magnetic field, an alternating emf is induced in the coil.
• The main components of the AC generator are:
  1. Armature
  2. Strong field magnet
  3. Slip rings
  4. Brushes
• When the armature coil ABCD rotates in the magnetic field provided by the strong field magnet, it cuts the magnetic lines of force.
• Thus the magnetic flux linked with the coil changes and hence induced emf is set up in the coil.
• The direction of the induced emf or the current in the coil is determined by Fleming’s right-hand rule.
• The current flows out through the brush B1 in the first half of the revolution and through the brush B2 in the next half revolution of the coil.
• This process is repeated. Therefore, emf produced is of alternating nature.
• The coil of the AC generator is rotated with a constant angular speed ω, the angle between the magnetic field vector B and the area vector A of the coil at any instant t is θ. Then,

⇒ θ = ωt

The flux linked with the coil at any time t is,

⇒ ϕ = BA.cosθ

• From Faraday’s law, the induced emf at any time t for the rotating coil of N turns is given as,

⇒ ϵ = NBAω.sin(ωt)

• If the resistance of the coil is R, then the induced current at any time t for the rotating coil of N turns is given as,

$\Rightarrow I=\frac{ϵ}{R}=\frac{NBA\omega sin(\omega t)}{R}$

CALCULATION:

Given A = 2.5 m2, N = 800 turns, ω = 50 rad/sec, B = 0.05 T, and R = 200 Ω

Where A = area of the coil, N = number of turns, R = resistance, ω = angular speed of coil, and B = magnetic field

• We know that the maximum current induced in the AC generator is given as,

$\Rightarrow I_{max}=\frac{NBA\omega }{R}$

$\Rightarrow I_{max}=\frac{800\times 0.05\times 2.5\times 50}{200}$

⇒ I_max = 25 A

• Hence, option 1 is correct.

Concept:

LCR Circuit: The ac circuit containing the capacitor, resistor, and inductor is called an LCR circuit.

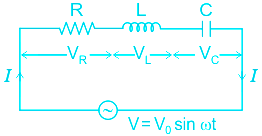
For a series LCR circuit, Impedance (Z) of the circuit is given by:

$$$Z=\surd R^2+{\left(X_L-X_C\right)}^2$
Where R = Resistance, XL = Inductive reactance, XC = Capacitive reactive

If the voltage drop across the three is the same, then R = X_L = X_C 

Calculation:

Given:

V_R = VL = VC = 10 V

As the voltage drop across the three is the same, then R = XL = XC

If the capacitor is shorted then

R = XL 

Impedance, $Z=\surd R^2+{\left(X_L-X_C\right)}^2$

$Z=\surd R^2+{\left(R-0\right)}^2$

Z = R√2

So the current in the circuit

I = $\frac{V}{Z}=\frac{10}{R\sqrt{2}}$

Also, VL = IXL 

VL = $\frac{10}{R\sqrt{2}}\times R$   (∵ XL = R)

VL = $\frac{10}{\sqrt{2}}$  V

Additional Information Power factor (Cos Φ): The ratio of the true power to the apparent power of an a.c. the circuit is called the power factor.

• Its value varies from 0 to 1.

The power factor (P) of a series LCR-circuit is given by:  

$\cos \mathrm{\Phi }=\frac{R}{Z}=\frac{R}{\surd R^2+{\left(X_L-X_C\right)}^2}$

Where R = resistance, Z = Impedance, XL = Inductive reactance and XC = Capacitive reactance

Concept:

The quality factor Q is defined as the ratio of the resonant frequency to the bandwidth.

$Q=\frac{f_r}{BW}=\frac{1}{R}\sqrt{\frac{L}{C}}$

fr = Resonant frequency

BW = Bandwidth of the resonant circuit

Calculation:

Given fr = 160 kHz

Q = 100

$BW=\frac{f_r}{Q}$

Bandwidth = $\frac{160kHz}{100}=1.6kHz$

The sharpness of the resonance in RLC series resonant circuit is measured by the quality factor and is explained in the figure shown below:

Observations:

• Less the Bandwidth, more the Quality factor.
• More the Bandwidth, less is the Quality factor.
• For the above figure, B2 > B1, so Q2 < Q1